

$20.$深海机器人问题

题目

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。

潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。

深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。

每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。

本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。

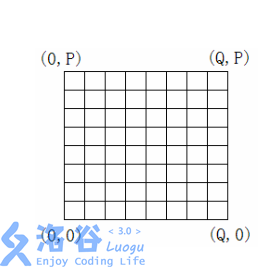
用一个$P\times Q$网格表示深海机器人的可移动位置。西南角的坐标为$(0,0)$，东北角的坐标为$(Q,P)$。

给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。

计算深海机器人的最优移动方案， 使深海机器人到达目的地后，采集到的生物标本的总价值最高。

题解

其实挺水，但是我发现两个问题。

• 边的编号要从$2$开始，不然反边加不了，我总是忘。
• 最大费用最大流最好还是边权取相反数然后最小费用最大流再反过来靠谱一点，我直接写在松弛操作中不对。

就简单的讲一下一个点$u$到另一个点$v$（假设$u$在$v$的西方或南方）之间有$val$权值，应该如何连边。

1. 首先新建一个点$x$,连边由$u$向$x$连一条$(1,val)$，由$x$向$v$连一条$(1,0)$。
2. 再新建一个点$y$,连边由$u$向$y$连一条$(inf,0)$，由$y$向$v$连一条$(inf,0)$。

为什么这么建就不用多说了。

最大费用即为结果。