

$16.$数字梯形问题

题目

给定一个由 $n$ 行数字组成的数字梯形如下图所示。

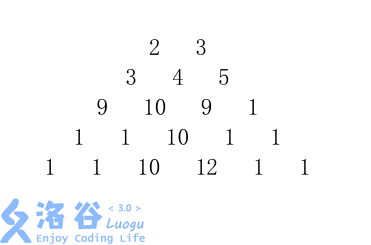
梯形的第一行有 $m$ 个数字。从梯形的顶部的 $m$ 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。

分别遵守以下规则：

1. 从梯形的顶至底的 $m$ 条路径互不相交；
2. 从梯形的顶至底的 $m$ 条路径仅在数字结点处相交；
3. 从梯形的顶至底的 $m$ 条路径允许在数字结点相交或边相交。

题解

题目很水，不用多说。

考虑对于那种不能相交的东西（比如节点，路径），考虑如何建图中表示出来，不能相交，说明只能走一次，那么就_{按照一贯套路，}将他们拆成两个点，连边流量为$1$,可以相交的就连边无限大。

接下来是三种情况分别如何连边（都是有向的）：

1. 把一个点$u$拆成两个点$u_1,u_2$, $u_1$向$u_2$连边$(1,a[u])$,即流量$1$,费用（或者说是贡献）$a[u]$,若两个点之间由连边（由上向下面的两个点），就由$u_2$向$v_1$连边$(1,0)$,$S$向最上面一层$m$个点连边$(1,0)$,最下面一层点向$T$连边$(1,0)$。
2. 只需要改部分边的容量，$u_1$与$u_2$之间的边容量改为$inf$,因为点可以多次经过，最下面一层的点$v_2$与$T$的连边改为$inf$

，原因一样。

1. 所有边容量都改为$inf$,但是$S$到最上面一层点$u_1$容量为$1$，因为无论怎样最上面每个点最多且必须用一次。

跑最大费用最大流后最大费用就是结果。