

$15.$汽车加油问题

题目

给定一个 $N \times N$ 的方形网格，设其左上角为起点◎，坐标 $(1,1)$ ， $X$ 轴向右为正， $Y$ 轴向下为正，每个方格边长为 $1$ ，如图所示。

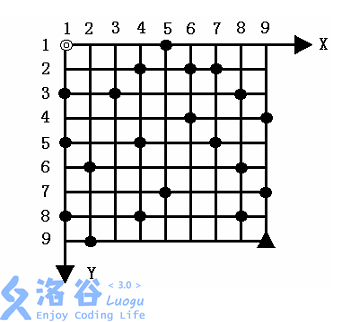
一辆汽车从起点◎出发驶向右下角终点▲，其坐标为 $(N,N)$。

在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:

1. 汽车只能沿网格边行驶，装满油后能行驶 $K$ 条网格边。出发时汽车已装满油，在起点与终点处不设油库。
2. 汽车经过一条网格边时，若其 $X$ 坐标或 $Y$ 坐标减小，则应付费用 $B$ ，否则免付费用。
3. 汽车在行驶过程中遇油库则应加满油并付加油费用 $A$ 。
4. 在需要时可在网格点处增设油库，并付增设油库费用 $C$ (不含加油费用 $A$ )。
5. $N,K,A,B,C$均为正整数， 且满足约束: $2\leq N\leq 100,2 \leq K \leq 10$。

设计一个算法，求出汽车从起点出发到达终点所付的最小费用。

题解

其实非常水，其实不需要用到网络流。

由于一个点的移动也可以看成同时存在的油箱内油的变化，所以可以按照油箱内的油量来分层。

到达点 $i$ ,剩余油量为$l$时，将这个状态表示为一个点 $<i,l>$ ,它处在的层肯定就是第$l$ 层，然后加边的方法就贴一下 BYVoid的吧。

1. 如果油箱不满$(l<K)$ ，点$i$为油库点，从 $<i,l>$ 到 $<i,K>$ 建立一条权值为$A$的有向边。
2. 如果油箱不满$(l<K)$ ，点$i$不为油库点，从 $<i,l>$ 到 $<i,K>$ 建立一条权值为A+C的有向边。
3. 如果油箱不为空， $i$ 不为油库点，每层 $l$ 从$<i,l>$到$<j,l-1>$建立一条权值为0的有向边，其中j为i的右边或下边相邻的一个顶点；从 $<i,l>$ 到 $<j,l-1>$ 建立一条权值为B的有向边，其中j为i的左边或上边相邻的一个顶点。
4. 如果油箱不为空，$i$ 为油库点，从 $<i,K>$ 到 $<j,K-1>$ 建立一条权值为0的有向边，其中j为i的右边或下边相邻的一个顶点；从 $<i,K>$ 到 $<j,K-1>$ 建立一条权值为B的有向边，其中j为i的左边或上边相邻的一个顶点。

求最短路之后答案就是 $min\{dis[<N,N,k>]|0\leq k \leq K\}$